《咸鱼之王》破甲和减伤两大属性各个阶段的收益（数据函数分析）

设f(x)为在x%破甲时每增加1%破甲的收益提升函数

则有f(x)={[(100-70+x+1)/(100-70+x)]-1}*100%,(0≤x≤70)

作为对照组，我们引进g(x)函数

设g(x)为在x%攻击时每增加1%攻击的收益提升函数

易知g(x)=x/x=1，为常数

翻译翻译就是我前面的文章里提到的攻击收益恒定原则，基础数值的计算方式是乘算，因此无论基数多大，收益永远是最为基础的1:1。

下面是破甲收益与攻击收益的对照图：

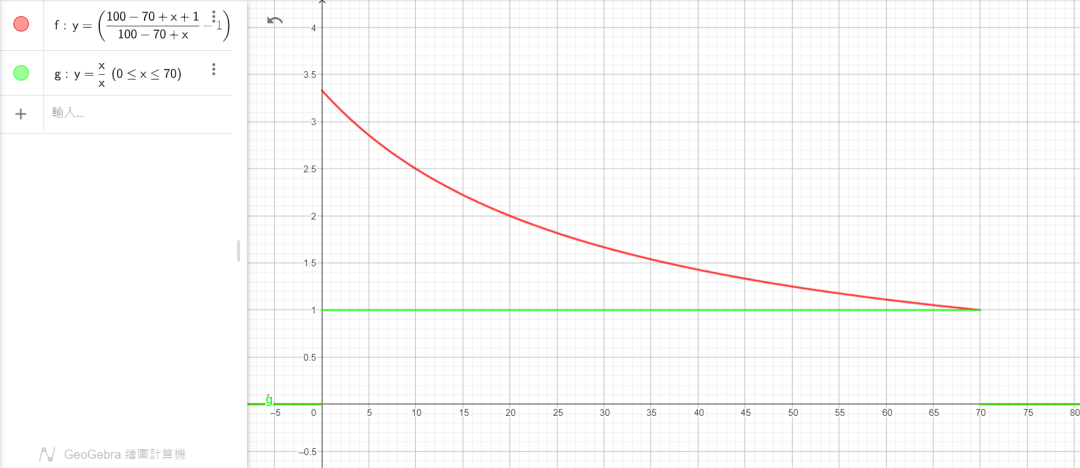
红色为破甲收益函数，绿色为攻击收益函数

由图可知，破甲（生效的前提下）在0-70的区间内收益的数学期望是斜率递减的单调递减函数。破甲在刚刚生效的时候，收益达到顶峰，为惊人的1:3.333，此后虽然在下降，但始终高于攻击的收益，最终在70的时候等于攻击的收益。

再设f(x)为在x%减伤时每增加1%减伤的收益提升函数

则有f(x)={[(100-x)/(100-(x+1))]-1}*100%,(0≤x≤70)

同样引进攻击收益函数g(x)为对照组。

如图所示：

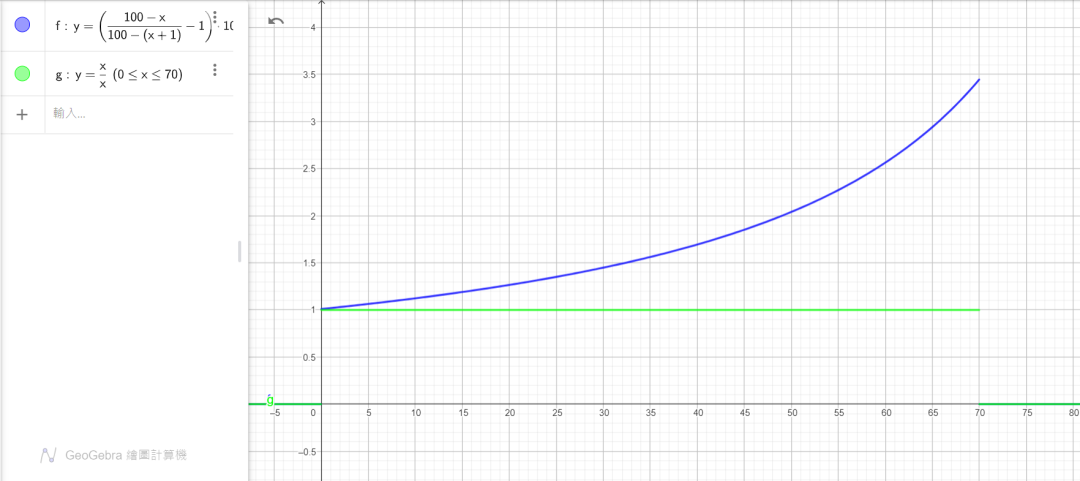
蓝色为减伤收益函数，绿色为攻击收益函数

由图可知，减伤在0-70的区间内收益的数学期望是斜率递增的单调递增函数。减伤在刚开始生效的时候收益无限趋近于攻击（或血量），随着越来越接近70这个阈值而陡然增加收益，70时达到极大值，同样为1:3.333。

省流总结：减伤一定要满，越到后面增益越夸张；破甲一定要有，只要生效收益就很大，且不一定追满，有效破甲在60%左右就已经吃到了破甲的绝大部分收益。